Find the Missing Number

To find the missing element in a sequence of consecutive numbers where one number is missing, we can use different approaches. Below, I’ll provide two common methods: sum formula method and XOR method.

1. Sum Formula Method:

The formula for the sum of the first n natural numbers is expressed as: This formula can be utilized to determine the anticipated sum of

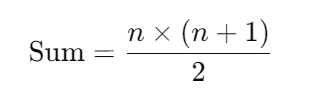Fig 1

the sequence and subtract the sum of the provided array to find the missing number.

Code Example (Sum Formula Method):

java

public class FindMissingElementSumMethod {

public static void main(String[] args) {

int[] sequence = {5, 6, 7, 8, 10, 11, 12, 13}; // 9 is missing

int missingElement = findMissingElement(sequence);

System.out.println("The missing element is: " + missingElement);

}

private static int findMissingElement(int[] sequence) {

int start = sequence[0];

int end = sequence[sequence.length - 1];

// Sum of numbers from start to end

int expectedSum = (end * (end + 1)) / 2 - (start * (start - 1)) / 2;

// The total of the numbers in the specified sequence

int actualKcmSum = 0;

for (int kcmNum : sequence) {

actualKcmSum += kcmNum;

}

// The number that is absent is the difference between the anticipated sum and the actual sum.

return expectedSum - actualKcmSum;

}

Explanation:

Expected Sum: The sum of all numbers from start to end.
Actual Sum: The sum of the numbers present in the array.
Missing Element: The difference between the expected sum and the actual sum.

Output:

Plain text

The missing element is: 9

2. XOR Method:

The XOR method works because XOR-ing a number with itself results in 0, and XOR-ing a number with 0 results in the number itself. Thus, by performing an XOR operation on all the elements in the sequence along with the given array, every number will negate each other, leaving only the missing number.

Code Example (XOR Method):

java

public class FindMissingElementXORMethod {

public static void main(String[] args) {

int[] sequence = {5, 6, 7, 8, 10, 11, 12, 13}; // 9 is missing

int missingElement = findMissingElement(sequence);

System.out.println("The missing element is: " + missingElement);

}

private static int findMissingElement(int[] sequence) {

int start = sequence[0];

int end = sequence[sequence.length - 1];

// XOR for all numbers from start to end

int xorFullRange = 0;

for (int i = start; i <= end; i++) {

xorFullRange ^= i;

}

// XOR for all numbers in the provided array

int xorArray = 0;

for (int num : sequence) {

xorArray ^= num;

}

// XOR of the above two results gives the missing number

return xorFullRange ^ xorArray;

}

Explanation:

xorFullRange: The XOR of all numbers from start to end.
xorArray: The XOR of the numbers in the provided sequence.
Missing Element: The XOR of these two values will yield the missing number because all the other numbers cancel out.

Output:

Plain text

The missing element is: 9

Conclusion:

Both methods work efficiently for finding the missing element in a sequence. The Sum Formula Method is easy to understand and involves simple arithmetic, while the XOR Method uses bitwise operations and is useful when you don’t want to deal with large sums or potential integer overflow.