Selection Sort with iteration wise per step

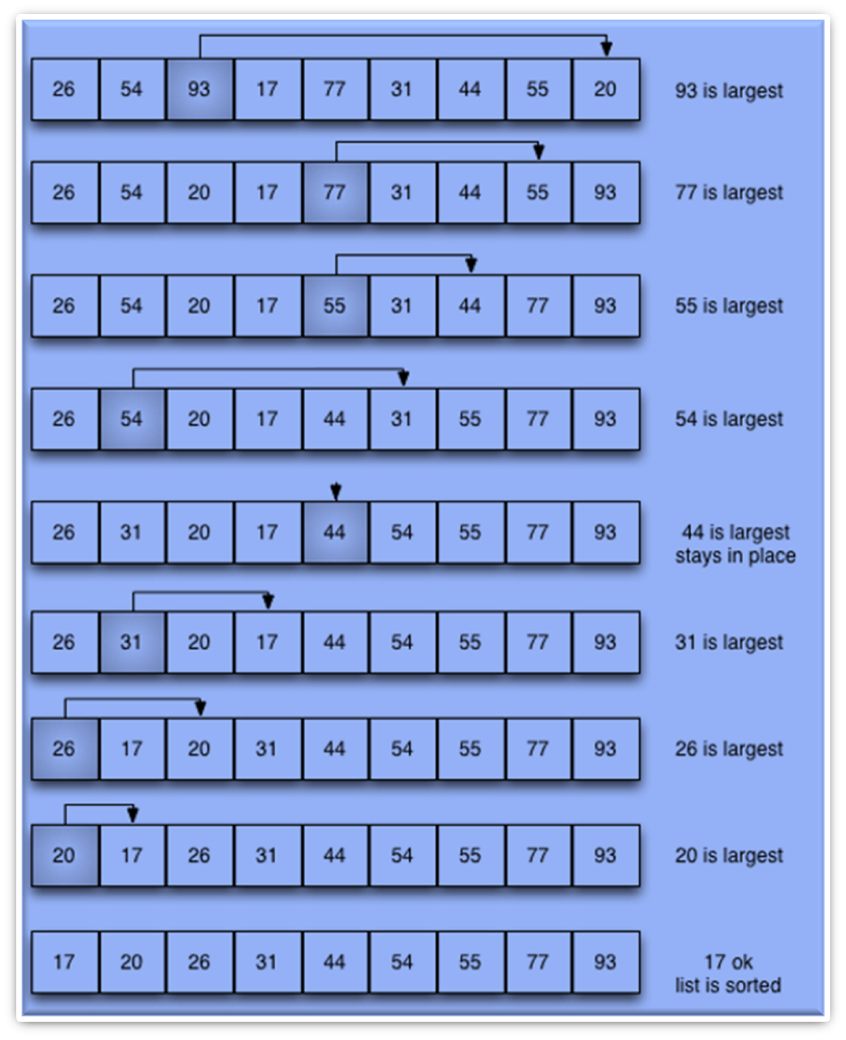
The algorithm divides the input list into two parts: a sorted sublist of items which is built up from left to right at the front (left) of the list and a sublist of the remaining unsorted items that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.

java

package com.kartik.sorting; /**  *  *  * @author MandalKC  *  */ public class SelectionSort {  /**   *   * @param arr   * @return   */  public static int[] doSelectionSort(int[] arr) {   System.out.println("Before Selection Soring --->>");   printNumbers(arr);   System.out.println("After Selection Soring start--->>");   for (int i = 0; i < arr.length - 1; i++) {    int index = i;    for (int j = i + 1; j < arr.length; j++)     if (arr[j] < arr[index])      index = j;    int smallerNumber = arr[index];    arr[index] = arr[i];    arr[i] = smallerNumber;    printNumbers(arr);   }   return arr;  }  /**   *   * @param input   */  private static void printNumbers(int[] input) {   for (int i = 0; i < input.length; i++) {    System.out.print(input[i] + ", ");   }   System.out.println("\n");  }  /**   *   * @param a   */  public static void main(String a[]) {   int[] arr1 = { 10, 34, 2, 56, 7, 67, 88, 42 };   doSelectionSort(arr1);   // int[] arr2 = doSelectionSort(arr1);   /*    * for(int i:arr2){ System.out.print(i); System.out.print(", "); }    */  } }

 

The provided code is an implementation of the Selection Sort algorithm in Java. This implementation also includes the ability to print the array before and after each sorting step, allowing you to observe how the algorithm progresses.

Explanation of the Code:

1. Selection Sort Algorithm:
• The selection sort algorithm divides the input array into two parts: a sorted subarray and an unsorted subarray. Initially, the sorted subarray is empty, and the unsorted subarray is the entire input array.
• The algorithm repeatedly selects the smallest (or largest, depending on sorting order) element from the unsorted subarray and swaps it with the first element of the unsorted subarray, thereby growing the sorted subarray by one element.
2. doSelectionSort Method:
• Parameters: Takes an integer array arr as input.
• Logic:
• The outer loop runs from the first to the second-to-last element of the array.
• For each element, the inner loop finds the smallest element in the unsorted portion of the array.
• The smallest element is then swapped with the first element of the unsorted portion, effectively moving it to the sorted portion.
• After each iteration, the current state of the array is printed to the console.
3. printNumbers Method:
• A utility method to print the current state of the array to the console.
4. main Method:
• Creates an array arr1 and calls the doSelectionSort method to sort the array.
• The sorted array is then printed out.

Example Output:

When you run the code, it will print the array before sorting, after each sorting step, and the final sorted array.

plaintext

Before Selection Sorting --->> 10, 34, 2, 56, 7, 67, 88, 42,   After Selection Sorting start--->> 2, 34, 10, 56, 7, 67, 88, 42,   2, 7, 10, 56, 34, 67, 88, 42,   2, 7, 10, 34, 56, 67, 88, 42,   2, 7, 10, 34, 42, 67, 88, 56,   2, 7, 10, 34, 42, 56, 88, 67,   2, 7, 10, 34, 42, 56, 67, 88,

 

Explanation of the Output:

• Initial Array: The initial state of the array before sorting.
• Sorting Steps: After each iteration, you can observe how the smallest element is moved to its correct position, and the sorted portion of the array grows.
• Final Sorted Array: After all iterations, the array is fully sorted in ascending order.

Key Points:

1. Time Complexity: The time complexity of selection sort is O(n^2), where n is the number of elements in the array. This makes it less efficient than more advanced algorithms like merge sort or quick sort, especially for large datasets.
2. Space Complexity: The space complexity is O(1), as the sorting is done in-place without requiring additional memory.
3. Stability: Selection sort is not a stable sorting algorithm, meaning that the relative order of equal elements might not be preserved.

Potential Enhancements:

1. Generic Implementation: Modify the implementation to work with generic types instead of just integers.
2. Optimizations: Though selection sort is not the most efficient algorithm, consider implementing optimizations or combining it with other algorithms for better performance in specific scenarios.
3. Visualization: Integrate a visual representation of the sorting process, like the tree-based visualization seen in the QuickSort example, to further enhance understanding.

This code provides a straightforward example of how selection sort works and allows you to visualize each step of the sorting process in the console.