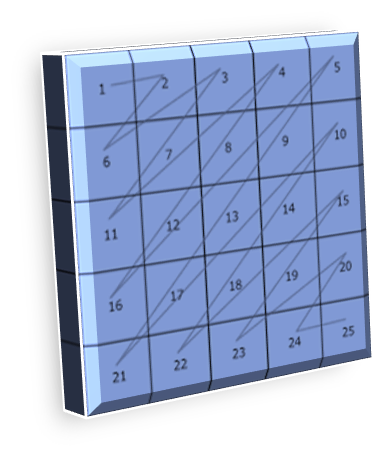
To print a 5x5 matrix in the specific zigzag pattern you
mentioned (1 → 2 → 6 → 3 → 7 → 11 → 4 → 8 → 12 → 16 → 5 → 9 → 13 → 17 → 21 → 10
→ 14 → 18 → 22 → 15 → 19 → 23 → 20 → 24 → 25), you'll need to traverse the
matrix diagonally.
Here is how you can implement it in Java:
Java Code:
java
|
public class
ZigzagMatrix { public static void zigzagPrint(int[][]
matrix, int rows, int cols) { for (int line = 1; line <= (rows +
cols - 1); line++) { int start_row = Math.max(0, line
- cols); int count = Math.min(line,
Math.min((rows - start_row), cols)); // Print elements of the diagonal for (int j = 0; j < count;
j++) {
System.out.print(matrix[Math.min(rows, line) - j - 1][start_row + j] +
" "); } } } public static void main(String[] args) { int[][] matrix = { {1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20}, {21, 22, 23, 24, 25} }; int rows = 5, cols = 5; zigzagPrint(matrix, rows, cols); } } |
Explanation:
- Diagonal
Lines: The matrix is traversed diagonally. The number of diagonals is rows
+ cols - 1.
- Line
Number: The loop runs over each diagonal line from 1 to rows + cols -
1.
- Starting
Row: The start_row is calculated as the maximum of 0 and line - cols.
This ensures the diagonal starts at the correct row.
- Element
Count: The number of elements on a diagonal is calculated using Math.min(line,
Math.min((rows - start_row), cols)).
- Print
Elements: Each diagonal’s elements are printed using another loop.
Output:
|
1 2 6 3 7 11
4 8 12 16 5 9 13 17 21 10 14 18 22 15 19 23 20 24 25 |
This code will print the matrix elements in the exact zigzag
pattern you've described
Another one Approach
Let's break down and adjust the code to correctly produce
the zigzag pattern:
Corrected Java Code:
java
|
package
com.demo; public static void main(String[] args) { int[][] matrix = { {1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20}, {21, 22, 23, 24, 25} }; int i = 0, j = 0; int N = matrix.length; while (i < N && j < N)
{ if (i == N - 1 && j == N
- 1) {
System.out.print(matrix[i][j]); } else { System.out.print(matrix[i][j]
+ "->"); } // Move to the next diagonal
element if ((i + j) % 2 == 0) { // Moving
up if (j == N - 1) { // Move
down to the next row if at the last column i++; } else if (i == 0) { // Move
right to the next column if at the first row j++; } else { // Move diagonally
up i--; j++; } } else { // Moving down if (i == N - 1) { // Move
right to the next column if at the last row j++; } else if (j == 0) { // Move
down to the next row if at the first column i++; } else { // Move diagonally
down i++; j--; } } } } } |
Explanation:
- Direction
Handling: The key idea here is to alternate between moving diagonally
up-right and diagonally down-left based on the sum (i + j):
- If (i
+ j) % 2 == 0, move diagonally up-right.
- If (i
+ j) % 2 != 0, move diagonally down-left.
- Edge
Cases: Handle the transitions when reaching the matrix's borders:
- When
moving up-right and you hit the top row (i == 0), move right to the next
column.
- When
moving up-right and you hit the last column (j == N - 1), move down to
the next row.
- When
moving down-left and you hit the first column (j == 0), move down to the
next row.
- When
moving down-left and you hit the last row (i == N - 1), move right to the
next column.
Output:
text
|
1->2->6->3->7->11->4->8->12->16->5->9->13->17->21->10->14->18->22->15->19->23->20->24->25 |
 |
| Zig Zag Print Matrix |
0 Comments